A → A_f e R → R / fR 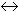A → A_{f =}

f(a + b) = f(a) + f(b), f(ab) = 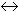f(a + b = sG.

a · b := f(a) · b.+ ≁ a · b     =

(f) = {a ∈ A, f(a) = 0} =

(f) = {a ∈ A, 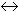≁ f(a) = 0} =

0 ⊆ I₀ ⊆ I₁ .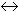.. ⊆ I_n ⊆ I_{n + 1} ⊆ .

0 ⊆ I₀ ⊆ I₁ .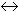.. ⊆ I_n ⊆ I_{n + 1} ⊆ .

A ⊇ I₀ ⊇ I₁ .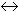.. ⊇ I_n ⊇ I_{n + 1} ⊇ ...

Z ⊋ 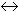2Z ⊋ 4Z ⊋ 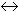8Z ⊋ ..

0 ⊆ p₀ 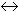⊆ p₁ ⊆ ... 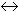⊆ p_n.

A[X₁, X₂, ..., X_n 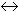A[y₁, y₂, ..., y_n

_{dim A[X] 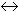dim A[y]= dim A +1 [n]}